Fortran MAXLOC SVP64 demo
https://bugs.libre-soc.org/show_bug.cgi?id=676
MAXLOC is a notoriously difficult function for SIMD to cope with. Typical approaches are to perform leaf-node (depth-first) parallel operations, merging the results mapreduce-style to guage a final index.
SVP64 however has similar capabilities to Z80 CPIR and LDIR and therefore hardware may transparently implement back-end parallel operations whilst the developer programs in a simple sequential algorithm.
A clear reference implementation of MAXLOC is as follows:
int maxloc(int * const restrict a, int n) {
int m, nm = INT_MIN, 0;
for (int i=0; i<n; i++) {
if (a[i] > m) {
m = a[i];
nm = i;
}
}
return nm;
}
AVX-512
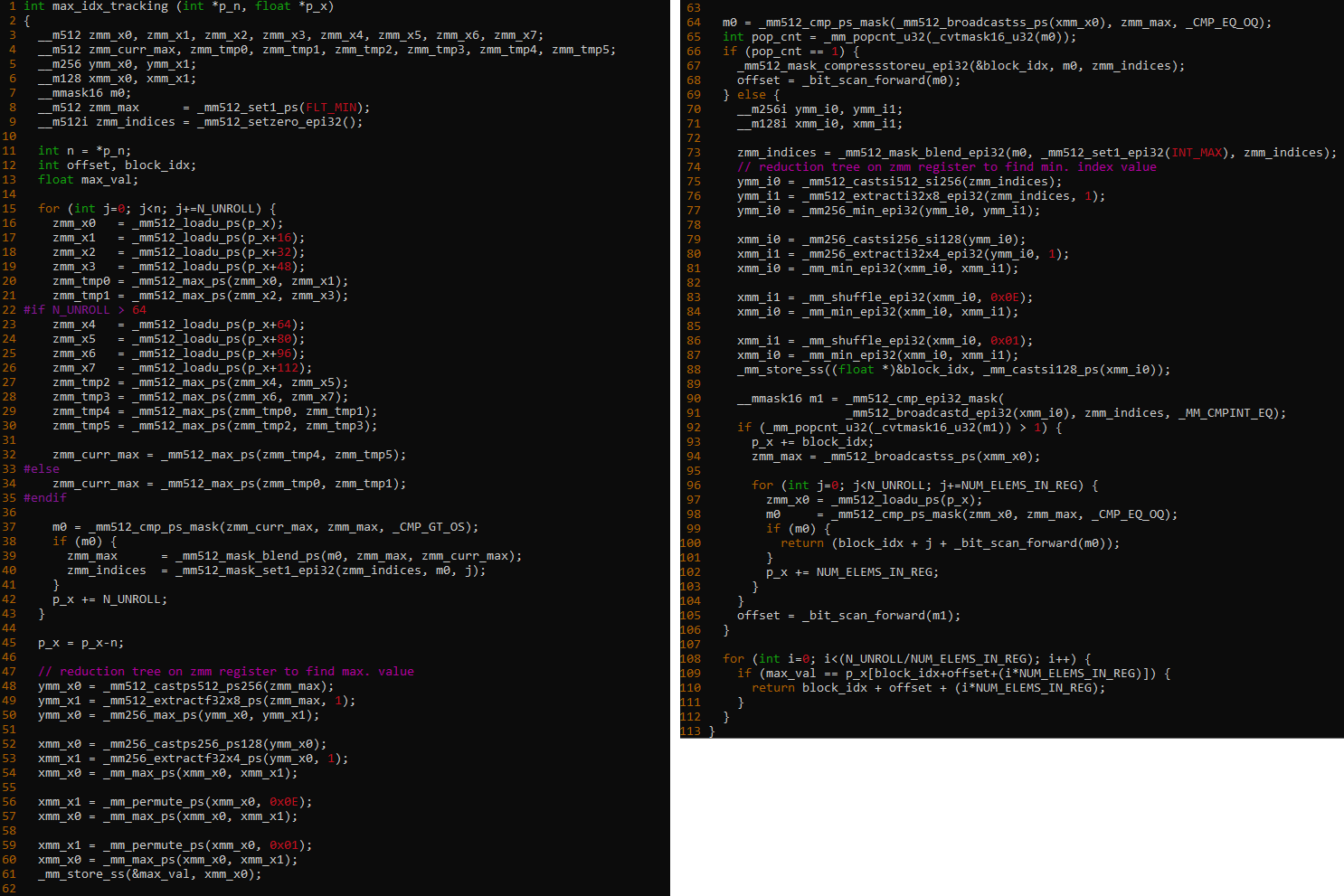
An informative article by Vamsi Sripathi of Intel shows the extent of the problem faced by SIMD ISAs (in the case below, AVX-512). Significant loop-unrolling is performed which leaves blocks that need to be merged: this is carried out with "blending" instructions.
ARM NEON
From stackexchange in ARM NEON intrinsics, one developer (Pavel P) wrote the subroutine below, explaining that it finds the index of a minimum value within a group of eight unsigned bytes. It is necessary to use a second outer loop to perform many of these searches in parallel, followed by conditionally offsetting each of the block-results.
#define VMIN8(x, index, value) \
do { \
uint8x8_t m = vpmin_u8(x, x); \
m = vpmin_u8(m, m); \
m = vpmin_u8(m, m); \
uint8x8_t r = vceq_u8(x, m); \
\
uint8x8_t z = vand_u8(vmask, r); \
\
z = vpadd_u8(z, z); \
z = vpadd_u8(z, z); \
z = vpadd_u8(z, z); \
\
unsigned u32 = vget_lane_u32(vreinterpret_u32_u8(z), 0); \
index = __lzcnt(u32); \
value = vget_lane_u8(m, 0); \
} while (0)
uint8_t v[8] = { ... };
static const uint8_t mask[] = { 0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01 };
uint8x8_t vmask = vld1_u8(mask);
uint8x8_t v8 = vld1_u8(v);
int ret;
int ret_pos;
VMIN8(v8, ret_pos, ret);
Rust Assembler Intrinsics
An approach by jvdd shows that the two stage approach of "blending" arrays of results in a type of parallelised "leaf node depth first" search seems to be a common technique.
https://github.com/jvdd/argminmax/blob/main/src/simd/simd_u64.rs
Python implementation
A variant on the c reference implementation allows for skipping of updating m (the largest value found so far), followed by always updating m whilst a batch of numbers is found that are (in their order of sequence) always continuously greater than all previous numbers. The algorithm therefore flips back and forth between "skip whilst smaller" and "update whilst bigger", only updating the index during "bigger" sequences. This is key later when doing SVP64 assembler.
def m2(a): # array a
m, nm, i, n = 0, 0, 0, len(a)
while i<n:
while i<n and a[i]<=m: i += 1 # skip whilst smaller/equal
while i<n and a[i]> m: m,nm,i = a[i],i,i+1 # only whilst bigger
return nm
Implementation in SVP64 Assembler
The core algorithm (inner part, in-register) is below: 11 instructions. Loading of data, and offsetting the "core" below is relatively straightforward: estimated another 6 instructions and needing one more branch (outer loop).
# while (i<n)
setvl 2,0,4,0,1,1 # set MVL=4, VL=MIN(MVL,CTR)
# while (i<n and a[i]<=m) : i += 1
sv.cmp/ff=gt/m=ge *0,0,*10,4 # truncates VL to min
sv.creqv *16,*16,*16 # set mask on already-tested
setvl 2,0,4,0,1,1 # set MVL=4, VL=MIN(MVL,CTR)
mtcrf 128, 0 # clear CR0 (in case VL=0?)
# while (i<n and a[i]>m):
sv.minmax./ff=le/m=ge/mr 4,*10,4,1 # uses r4 as accumulator
sv.crnand/m=lt/zz *19,*16,0 # SO=~LT, if CR0.eq=0
# nm = i (count masked bits. could use crweirds here TODO)
sv.svstep/mr/m=so 1, 0, 6, 1 # svstep: get vector dststep
sv.creqv *16,*16,*16 # set mask on already-tested
bc 12,0, -0x3c # CR0 lt bit clear, branch back
sv.cmp can be used in the first while loop because m (r4, the current
largest-found value so far) does not change.
However sv.minmax. has to be used in the key while loop
because r4 is sequentially replaced each time, and mapreduce (/mr)
is used to request this rolling-chain (accumulator) mode.
Also note that i (the "while i<n" part) is represented as an
unary bitmask (in CR bits 16,20,24,28) which turns out to be easier to
use than a binary index, as it can be used directly as a Predicate Mask
(/m=ge).
The algorithm works by excluding previous operations using i-in-unary,
combined with VL being truncated due to use of Data-Dependent Fail-First.
What therefore happens for example on the sv.cmp/ff=gt/m=ge operation
is that it is VL (the Vector Length) that gets truncated to only
contain those elements that are smaller than the current largest value
found (m aka r4). Calling sv.creqv then sets only the
CR field bits up to length VL, which on the next loop will exclude
them because the Predicate Mask is m=ge (ok if the CR field bit is
zero).
Therefore, the way that Data-Dependent Fail-First works, it attempts
up to the current Vector Length, and on detecting the first failure
will truncate at that point. In effect this is speculative sequential
execution of while (i<n and a[i]<=m) : i += 1.
Next comes the sv.minmax. which covers the while (i<n and a[i]>m)
again in a single instruction, but this time it is a little more
involved. Firstly: mapreduce mode is used, with r4 as both source
and destination, r4 acts as the sequential accumulator. Secondly,
again it is masked (m=ge) which again excludes testing of previously-tested
elements. The next few instructions extract the information provided
by Vector Length (VL) being truncated - potentially even to zero!
(Note that mtcrf 128,0 takes care of the possibility of VL=0, which if
that happens then CR0 would be left it in its previous state: a
very much undesirable behaviour!)
sv.crnand/m=lt/zz is quite sophisticated - a lot is going on behind
the scenes. The effect is (through the NAND) to invert the Less-than
to give us a Greater-than-or-equal, including under the circumstance
where VL=0, but only when CR0.EQ is set. Note that the third operand
BB (CR0.EQ) is a scalar, but that zeroing is used here. Therefore
whenever the Vector of LT bits is zero, a zero is put into the
Vector SO result. In effect, the predication is being exploited
as a way to combine a third operand into what would otherwise be a
2-in 1-out Condition Register operation, making it effectively 3-in 1-out.
Obscure but effective!
CR4.SO = CR4.EQ AND CR0.EQ (if VL >= 1)
CR5.SO = CR5.EQ AND CR0.EQ (if VL >= 2)
CR6.SO = CR6.EQ AND CR0.EQ (if VL >= 3)
CR7.SO = CR7.EQ AND CR0.EQ (if VL = 4)
Converting the unary mask to binary
Now that the CR4/5/6/7.SO bits have been set, it is necessary to
count them, i.e. convert an unary mask into a binary number. There
are several ways to do this, one of which is
the crweird suite of instructions, combined with popcnt. However
there is a very straightforward way to it: use sv.svstep.
sv.crnand/m=lt/zz *19,*16,0 # Vector SO = Vector ~LT, if CR0.eq=0
i ----> 0 1 2 3
CR4.EQ CR5.EQ CR6.EQ CR7.EQ
& CR0 & CR0 & CR0 & CR0
| | | |
v v v v
CR4.SO CR5.SO CR6.SO CR7.SO
sv.svstep/mr/m=so 1, 0, 6, 1
| | | |
count <--+---------+--------+---------+
In reality what is happening is that svstep is requested to return
the current dststep (destination step index), into a scalar
destination (RT=r1), but in "mapreduce" mode. Mapreduce mode
will keep running as if the destination was a Vector, overwriting
previously-written results. Normally, one of the sources would
be the same register (RA=r1 for example) which would turn r1 into
an accumulator, however in this particular case we simply consistently
overwrite r1 and end up with the last dststep.
There is an alternative to this approach: getvl followed by
subtracting 1. VL being the total Vector Length as set by
Data-Dependent Fail-First, is the length of the Vector, whereas
what we actually want is the index of the last element: hence
using sv.svstep. Given that using getvl followed by addi -1
is two instructions rather than one, we use sv.svstep instead,
although they are the same amount of words (SVP64 is 64-bit sized).
Lastly the creqv sets up the mask (based on the current
Vector Length), and the loop-back (bc) jumps to reset the
Vector Length back to the maximum (4). Thus, the mask (CR4/5/6/7 EQ
bit) which began as empty will exclude nothing but on subsequent
loops will exclude previously-tested elements (up to the previous
value of VL) before it was reset back to the maximum.
This is actually extremely important to note, here, because the Data-Dependent Fail-First testing starts at the first non-masked element, not the first element. This fact is exploited here, and the only thing to contend with is if VL is ever set to zero (first element fails). If that happens then CR0 will never get set, (because no element succeeded and the Vector Length is truncated to zero) hence the need to clear CR0 prior to starting that instruction.
Overall this algorithm is extremely short but quite complex in its intricate use of SVP64 capabilities, yet still remains parallelliseable in hardware. It could potentially be shorter: there may be opportunities to use predicate masking with the CR field manipulation. However the number of instructions is already at the point where, even when the LOAD outer loop is added it will still remain short enough to fit in a single line of L1 Cache.