1. Implementation Log
  2. bitmanipulation
  3. summary
  4. binary and ternary bitops
  5. int ops
  6. shift-and-add
  7. bitmask set
  8. grevlut
  9. grev
  10. gorc
  11. xperm
  12. bitmatrix
  13. Introduction to Carry-less and GF arithmetic
  14. Instructions for Carry-less Operations
  15. Instructions for Binary Galois Fields GF(2^m)
  16. Instructions for Prime Galois Fields GF(p)
  17. Already in POWER ISA or subsumed
  18. Appendix

Implementation Log

bitmanipulation

DRAFT STATUS

pseudocode: bitmanip

this extension amalgamates bitmanipulation primitives from many sources, including RISC-V bitmanip, Packed SIMD, AVX-512 and OpenPOWER VSX. Also included are DSP/Multimedia operations suitable for Audio/Video. Vectorisation and SIMD are removed: these are straight scalar (element) operations making them suitable for embedded applications. Vectorisation Context is provided by sv.

When combined with SV, scalar variants of bitmanip operations found in VSX are added so that the Packed SIMD aspects of VSX may be retired as "legacy" in the far future (10 to 20 years). Also, VSX is hundreds of opcodes, requires 128 bit pathways, and is wholly unsuited to low power or embedded scenarios.

ternlogv is experimental and is the only operation that may be considered a "Packed SIMD". It is added as a variant of the already well-justified ternlog operation (done in AVX512 as an immediate only) "because it looks fun". As it is based on the LUT4 concept it will allow accelerated emulation of FPGAs. Other vendors of ISAs are buying FPGA companies to achieve similar objectives.

general-purpose Galois Field 2M operations are added so as to avoid huge custom opcode proliferation across many areas of Computer Science. however for convenience and also to avoid setup costs, some of the more common operations (clmul, crc32) are also added. The expectation is that these operations would all be covered by the same pipeline.

note that there are brownfield spaces below that could incorporate some of the set-before-first and other scalar operations listed in vector ops, int fp mv and the av opcodes as well as setvl, svstep, remap

Useful resource:

summary

two major opcodes are needed

ternlog has its own major opcode

29.30 31 name Form
0 0 Rc ternlogi TLI-Form
0 1 crternlogi TLI-Form
1 iv grevlogi TLI-Form

2nd major opcode for other bitmanip: minor opcode allocation

28.30 31 name
-00 0 xpermi
-00 1 binary lut
-01 0 grevlog
-01 1 grevlogw
010 Rc bitmask
011 SVP64
110 Rc 1/2-op
111 bmrevi

1-op and variants

dest src1 subop op
RT RA .. bmatflip

2-op and variants

dest src1 src2 subop op
RT RA RB or bmatflip
RT RA RB xor bmatflip
RT RA RB grev
RT RA RB clmul*
RT RA RB gorc
RT RA RB shuf shuffle
RT RA RB unshuf shuffle
RT RA RB width xperm
RT RA RB type av minmax
RT RA RB av abs avgadd
RT RA RB type vmask ops
RT RA RB type abs accumulate (overwrite)

3 ops

  • grevlog[w]
  • GF mul-add
  • bitmask-reverse

TODO: convert all instructions to use RT and not RS

0.5 6.10 11.15 16.20 21..25 26....30 31 name Form
NN RT RA itype/ im0-4 im5-7 00 0 xpermi TLI-Form
NN RT RA RB RC nh 00 00 1 binlut VA-Form
NN RT RA RB /BFA/ 0 01 00 1 bincrflut VA-Form
NN 1 01 00 1 rsvd
NN - 10 00 1 rsvd
NN 0 11 00 1 svshape SVM-Form
NN 1 11 00 1 svremap SVRM-Form
NN RT RA RB im0-4 im5-7 01 0 grevlog TLI-Form
NN RT RA RB im0-4 im5-7 01 1 grevlogw TLI-Form
NN RT RA RB RC mode 010 Rc bitmask* VA2-Form
NN FRS d1 d0 d0 00 011 d2 fmvis DX-Form
NN FRS d1 d0 d0 01 011 d2 fishmv DX-Form
NN 10 011 Rc svstep SVL-Form
NN 11 011 Rc setvl SVL-Form
NN ---- 110 1/2 ops other table
NN RT RA RB sh0-4 sh5 1 111 Rc bmrevi MDS-Form

ops (note that av avg and abs as well as vec scalar mask are included here vector ops, and the av opcodes)

0.5 6.10 11.15 16.20 21 22.23 24....30 31 name Form
NN RS me sh SH ME 0 nn00 110 Rc bmopsi BM-Form
NN RS RA sh SH 0 1 nn00 110 Rc bmopsi XB-Form
NN 1 1 --00 110 Rc rsvd
NN RT RA RB 1 00 0001 110 Rc cldiv X-Form
NN RT RA RB 1 01 0001 110 Rc clmod X-Form
NN RT RA 1 10 0001 110 Rc clmulh X-Form
NN RT RA RB 1 11 0001 110 Rc clmul X-Form
NN RT RA RB 0 00 0001 110 Rc vec sbfm X-Form
NN RT RA RB 0 01 0001 110 Rc vec sofm X-Form
NN RT RA RB 0 10 0001 110 Rc vec sifm X-Form
NN RT RA RB 0 11 0001 110 Rc vec cprop X-Form
NN -0 0101 110 Rc crfbinlog {TODO}
NN -1 0101 110 Rc rsvd
NN RT RA RB 0 itype 1001 110 Rc av minmax X-Form
NN RT RA RB 1 00 1001 110 Rc av abss X-Form
NN RT RA RB 1 01 1001 110 Rc av absu X-Form
NN RT RA RB 1 10 1001 110 Rc av avgadd X-Form
NN RT RA RB 1 11 1001 110 Rc grevlutr X-Form
NN RT RA RB 0 itype 1101 110 Rc shadd X-Form
NN RT RA RB 1 itype 1101 110 Rc shadduw X-Form
NN RT RA RB 0 00 0010 110 Rc gorc X-Form
NN RS RA sh SH 00 1010 110 Rc gorci XB-Form
NN RT RA RB 0 00 0110 110 Rc gorcw X-Form
NN RS RA SH 0 00 1110 110 Rc gorcwi X-Form
NN RT RA RB 1 00 1110 110 Rc rsvd
NN RT RA RB 0 01 0010 110 Rc grev X-Form
NN RT RA RB 1 01 0010 110 Rc clmulr X-Form
NN RS RA sh SH 01 1010 110 Rc grevi XB-Form
NN RT RA RB 0 01 0110 110 Rc grevw X-Form
NN RS RA SH 0 01 1110 110 Rc grevwi X-Form
NN RT RA RB 1 01 1110 110 Rc rsvd
NN RS RA RB 0 10 0010 110 Rc bmator X-Form
NN RS RA RB 0 10 0110 110 Rc bmatand X-Form
NN RS RA RB 0 10 1010 110 Rc bmatxor X-Form
NN RS RA RB 0 10 1110 110 Rc bmatflip X-Form
NN RT RA RB 1 10 0010 110 Rc xpermn X-Form
NN RT RA RB 1 10 0110 110 Rc xpermb X-Form
NN RT RA RB 1 10 1010 110 Rc xpermh X-Form
NN RT RA RB 1 10 1110 110 Rc xpermw X-Form
NN RT RA RB 0 11 1110 110 Rc abssa X-Form
NN RT RA RB 1 11 1110 110 Rc absua X-Form
NN --11 110 Rc rsvd

binary and ternary bitops

Similar to FPGA LUTs: for two (binary) or three (ternary) inputs take bits from each input, concatenate them and perform a lookup into a table using an 8-8-bit immediate (for the ternary instructions), or in another register (4-bit for the binary instructions). The binary lookup instructions have CR Field lookup variants due to CR Fields being 4 bit.

Like the x86 AVX512F vpternlogd/vpternlogq instructions.

ternlogi

0.5 6.10 11.15 16.20 21..28 29.30 31
NN RT RA RB im0-7 00 Rc 
lut3(imm, a, b, c):
    idx = c << 2 | b << 1 | a
    return imm[idx] # idx by LSB0 order

for i in range(64): 
    RT[i] = lut3(imm, RB[i], RA[i], RT[i])

binlut

Binary lookup is a dynamic LUT2 version of ternlogi. Firstly, the lookup table is 4 bits wide not 8 bits, and secondly the lookup table comes from a register not an immediate.

0.5 6.10 11.15 16.20 21..25 26..31 Form
NN RT RA RB RC nh 00001 VA-Form
NN RT RA RB /BFA/ 0 01001 VA-Form

For binlut, the 4-bit LUT may be selected from either the high nibble or the low nibble of the first byte of RC:

lut2(imm, a, b):
    idx = b << 1 | a
    return imm[idx] # idx by LSB0 order

imm = (RC>>(nh*4))&0b1111
for i in range(64): 
    RT[i] = lut2(imm, RB[i], RA[i])

For bincrlut, BFA selects the 4-bit CR Field as the LUT2:

for i in range(64): 
    RT[i] = lut2(CRs{BFA}, RB[i], RA[i])

When Vectorised with SVP64, as usual both source and destination may be Vector or Scalar.

Programmer's note: a dynamic ternary lookup may be synthesised from a pair of binlut instructions followed by a ternlogi to select which to merge. Use nh to select which nibble to use as the lookup table from the RC source register (nh=1 nibble high), i.e. keeping an 8-bit LUT3 in RC, the first binlut instruction may set nh=0 and the second nh=1.

crternlogi

another mode selection would be CRs not Ints.

0.5 6.8 9.11 12.14 15.17 18.20 21.28 29.30 31
NN BT BA BB BC m0-2 imm 01 m3 
mask = m0-3,m4
for i in range(4):
    a,b,c = CRs[BA][i], CRs[BB][i], CRs[BC][i])
    if mask[i] CRs[BT][i] = lut3(imm, a, b, c)

This instruction is remarkably similar to the existing crops, crand etc. which have been noted to be a 4-bit (binary) LUT. In effect crternlogi is the ternary LUT version of crops, having an 8-bit LUT.

crbinlog

With ternary (LUT3) dynamic instructions being very costly, and CR Fields being only 4 bit, a binary (LUT2) variant is better

0.5 6.8 9.11 12.14 15.17 18.22 23...30 31
NN BT BA BB BC m0-m2 00101110 m3 
mask = m0-3,m4
for i in range(4):
    a,b = CRs[BA][i], CRs[BB][i])
    if mask[i] CRs[BT][i] = lut2(CRs[BC], a, b)

When SVP64 Vectorised any of the 4 operands may be Scalar or Vector, including BC meaning that multiple different dynamic lookups may be performed with a single instruction.

Programmer's note: just as with binlut and ternlogi, a pair of crbinlog instructions followed by a merging crternlogi may be deployed to synthesise dynamic ternary (LUT3) CR Field manipulation

int ops

min/m

required for the av opcodes

signed and unsigned min/max for integer. this is sort-of partly synthesiseable in svp64 with pred-result as long as the dest reg is one of the sources, but not both signed and unsigned. when the dest is also one of the srces and the mv fails due to the CR bittest failing this will only overwrite the dest where the src is greater (or less).

signed/unsigned min/max gives more flexibility.

uint_xlen_t min(uint_xlen_t rs1, uint_xlen_t rs2)
{ return (int_xlen_t)rs1 < (int_xlen_t)rs2 ? rs1 : rs2;
}
uint_xlen_t max(uint_xlen_t rs1, uint_xlen_t rs2)
{ return (int_xlen_t)rs1 > (int_xlen_t)rs2 ? rs1 : rs2;
}
uint_xlen_t minu(uint_xlen_t rs1, uint_xlen_t rs2)
{ return rs1 < rs2 ? rs1 : rs2;
}
uint_xlen_t maxu(uint_xlen_t rs1, uint_xlen_t rs2)
{ return rs1 > rs2 ? rs1 : rs2;
}

average

required for the av opcodes, these exist in Packed SIMD (VSX) but not scalar

uint_xlen_t intavg(uint_xlen_t rs1, uint_xlen_t rs2) {
     return (rs1 + rs2 + 1) >> 1:
}

abs

required for the av opcodes, these exist in Packed SIMD (VSX) but not scalar

uint_xlen_t intabs(uint_xlen_t rs1, uint_xlen_t rs2) {
     return (src1 > src2) ? (src1-src2) : (src2-src1)
}

abs-accumulate

required for the av opcodes, these are needed for motion estimation. both are overwrite on RS.

uint_xlen_t uintabsacc(uint_xlen_t rs, uint_xlen_t ra, uint_xlen_t rb) {
     return rs + (src1 > src2) ? (src1-src2) : (src2-src1)
}
uint_xlen_t intabsacc(uint_xlen_t rs, int_xlen_t ra, int_xlen_t rb) {
     return rs + (src1 > src2) ? (src1-src2) : (src2-src1)
}

For SVP64, the twin Elwidths allows e.g. a 16 bit accumulator for 8 bit differences. Form is RM-1P-3S1D where RS-as-source has a separate SVP64 designation from RS-as-dest. This gives a limited range of non-overwrite capability.

shift-and-add

Power ISA is missing LD/ST with shift, which is present in both ARM and x86. Too complex to add more LD/ST, a compromise is to add shift-and-add. Replaces a pair of explicit instructions in hot-loops.

uint_xlen_t shadd(uint_xlen_t rs1, uint_xlen_t rs2, uint8_t sh) {
    return (rs1 << (sh+1)) + rs2;
}

uint_xlen_t shadduw(uint_xlen_t rs1, uint_xlen_t rs2, uint8_t sh) {
    uint_xlen_t rs1z = rs1 & 0xFFFFFFFF;
    return (rs1z << (sh+1)) + rs2;
}

bitmask set

based on RV bitmanip singlebit set, instruction format similar to shift fixedshift. bmext is actually covered already (shift-with-mask rldicl but only immediate version). however bitmask-invert is not, and set/clr are not covered, although they can use the same Shift ALU.

bmext (RB) version is not the same as rldicl because bmext is a right shift by RC, where rldicl is a left rotate. for the immediate version this does not matter, so a bmexti is not required. bmrev however there is no direct equivalent and consequently a bmrevi is required.

bmset (register for mask amount) is particularly useful for creating predicate masks where the length is a dynamic runtime quantity. bmset(RA=0, RB=0, RC=mask) will produce a run of ones of length "mask" in a single instruction without needing to initialise or depend on any other registers.

0.5 6.10 11.15 16.20 21.25 26..30 31 name
NN RS RA RB RC mode 010 Rc bm*

Immediate-variant is an overwrite form:

0.5 6.10 11.15 16.20 21 22.23 24....30 31 name
NN RS RB sh SH itype 1000 110 Rc bm*i 
def MASK(x, y):
     if x < y:
         x = x+1
         mask_a = ((1 << x) - 1) & ((1 << 64) - 1)
         mask_b = ((1 << y) - 1) & ((1 << 64) - 1)
     elif x == y:
         return 1 << x
     else:
         x = x+1
         mask_a = ((1 << x) - 1) & ((1 << 64) - 1)
         mask_b = (~((1 << y) - 1)) & ((1 << 64) - 1)
     return mask_a ^ mask_b


uint_xlen_t bmset(RS, RB, sh)
{
    int shamt = RB & (XLEN - 1);
    mask = (2<<sh)-1;
    return RS | (mask << shamt);
}

uint_xlen_t bmclr(RS, RB, sh)
{
    int shamt = RB & (XLEN - 1);
    mask = (2<<sh)-1;
    return RS & ~(mask << shamt);
}

uint_xlen_t bminv(RS, RB, sh)
{
    int shamt = RB & (XLEN - 1);
    mask = (2<<sh)-1;
    return RS ^ (mask << shamt);
}

uint_xlen_t bmext(RS, RB, sh)
{
    int shamt = RB & (XLEN - 1);
    mask = (2<<sh)-1;
    return mask & (RS >> shamt);
}

bitmask extract with reverse. can be done by bit-order-inverting all of RB and getting bits of RB from the opposite end.

when RA is zero, no shift occurs. this makes bmextrev useful for simply reversing all bits of a register.

msb = ra[5:0];
rev[0:msb] = rb[msb:0];
rt = ZE(rev[msb:0]);

uint_xlen_t bmextrev(RA, RB, sh)
{
    int shamt = XLEN-1;
    if (RA != 0) shamt = (GPR(RA) & (XLEN - 1));
    shamt = (XLEN-1)-shamt;  # shift other end
    bra = bitreverse(RB)     # swap LSB-MSB
    mask = (2<<sh)-1;
    return mask & (bra >> shamt);
}
0.5 6.10 11.15 16.20 21.26 27..30 31 name
NN RT RA RB sh 1111 Rc bmrevi

grevlut

(3x lower latency alternative which is not equivalent and has limited constant-generation capability)

generalised reverse combined with a pair of LUT2s and allowing a constant 0b0101...0101 when RA=0, and an option to invert (including when RA=0, giving a constant 0b1010...1010 as the initial value) provides a wide range of instructions and a means to set hundreds of regular 64 bit patterns with one single 32 bit instruction.

the two LUT2s are applied left-half (when not swapping) and right-half (when swapping) so as to allow a wider range of options.

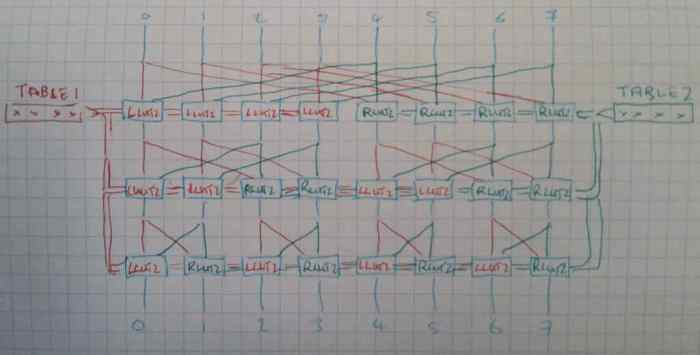
  • A value of 0b11001010 for the immediate provides the functionality of a standard "grev".
  • 0b11101110 provides gorc

grevlut should be arranged so as to produce the constants needed to put into bext (bitextract) so as in turn to be able to emulate x86 pmovmask instructions https://www.felixcloutier.com/x86/pmovmskb. This only requires 2 instructions (grevlut, bext).

Note that if the mask is required to be placed directly into CR Fields (for use as CR Predicate masks rather than a integer mask) then sv.cmpi or sv.ori may be used instead, bearing in mind that sv.ori is a 64-bit instruction, and VL must have been set to the required length:

sv.ori./elwid=8 r10.v, r10.v, 0

The following settings provide the required mask constants:

RA=0 RB imm iv result
0x555.. 0b10 0b01101100 0 0x111111...
0x555.. 0b110 0b01101100 0 0x010101...
0x555.. 0b1110 0b01101100 0 0x00010001...
0x555.. 0b10 0b11000110 1 0x88888...
0x555.. 0b110 0b11000110 1 0x808080...
0x555.. 0b1110 0b11000110 1 0x80008000...

Better diagram showing the correct ordering of shamt (RB). A LUT2 is applied to all locations marked in red using the first 4 bits of the immediate, and a separate LUT2 applied to all locations in green using the upper 4 bits of the immediate.

demo code grevlut.py

lut2(imm, a, b):
    idx = b << 1 | a
    return imm[idx] # idx by LSB0 order

dorow(imm8, step_i, chunksize, us32b):
    for j in 0 to 31 if is32b else 63:
        if (j&chunk_size) == 0
           imm = imm8[0..3]
        else
           imm = imm8[4..7]
        step_o[j] = lut2(imm, step_i[j], step_i[j ^ chunk_size])
    return step_o

uint64_t grevlut(uint64_t RA, uint64_t RB, uint8 imm, bool iv, bool is32b)
{
    uint64_t x = 0x5555_5555_5555_5555;
    if (RA != 0) x = GPR(RA);
    if (iv) x = ~x;
    int shamt = RB & 31 if is32b else 63
    for i in 0 to (6-is32b)
        step = 1<<i
        if (shamt & step) x = dorow(imm, x, step, is32b)
    return x;
}

A variant may specify different LUT-pairs per row, using one byte of RB for each. If it is desired that a particular row-crossover shall not be applied it is a simple matter to set the appropriate LUT-pair in RB to effect an identity transform for that row (0b11001010).

uint64_t grevlutr(uint64_t RA, uint64_t RB, bool iv, bool is32b)
{
    uint64_t x = 0x5555_5555_5555_5555;
    if (RA != 0) x = GPR(RA);
    if (iv) x = ~x;
    for i in 0 to (6-is32b)
        step = 1<<i
        imm = (RB>>(i*8))&0xff
        x = dorow(imm, x, step, is32b)
    return x;
}
0.5 6.10 11.15 16.20 21..28 29.30 31 name
NN RT RA s0-4 im0-7 1 iv s5 grevlogi
NN RT RA RB im0-7 01 0 grevlog |
NN RT RA RB im0-7 01 1 grevlogw |

grev

superceded by grevlut

based on RV bitmanip, this is also known as a butterfly network. however where a butterfly network allows setting of every crossbar setting in every row and every column, generalised-reverse (grev) only allows a per-row decision: every entry in the same row must either switch or not-switch.

uint64_t grev64(uint64_t RA, uint64_t RB)
{
    uint64_t x = RA;
    int shamt = RB & 63;
    if (shamt & 1) x = ((x &  0x5555555555555555LL) <<  1) |
                        ((x & 0xAAAAAAAAAAAAAAAALL) >>  1);
    if (shamt & 2) x = ((x &  0x3333333333333333LL) <<  2) |
                        ((x & 0xCCCCCCCCCCCCCCCCLL) >>  2);
    if (shamt & 4) x = ((x &  0x0F0F0F0F0F0F0F0FLL) <<  4) |
                        ((x & 0xF0F0F0F0F0F0F0F0LL) >>  4);
    if (shamt & 8) x = ((x &  0x00FF00FF00FF00FFLL) <<  8) |
                        ((x & 0xFF00FF00FF00FF00LL) >>  8);
    if (shamt & 16) x = ((x & 0x0000FFFF0000FFFFLL) << 16) |
                        ((x & 0xFFFF0000FFFF0000LL) >> 16);
    if (shamt & 32) x = ((x & 0x00000000FFFFFFFFLL) << 32) |
                        ((x & 0xFFFFFFFF00000000LL) >> 32);
    return x;
}

gorc

based on RV bitmanip, gorc is superceded by grevlut

uint32_t gorc32(uint32_t RA, uint32_t RB)
{
    uint32_t x = RA;
    int shamt = RB & 31;
    if (shamt & 1) x |= ((x & 0x55555555) << 1)   |  ((x &  0xAAAAAAAA) >> 1);
    if (shamt & 2) x |= ((x & 0x33333333) << 2)   |  ((x &  0xCCCCCCCC) >> 2);
    if (shamt & 4) x |= ((x & 0x0F0F0F0F) << 4)   |  ((x &  0xF0F0F0F0) >> 4);
    if (shamt & 8) x |= ((x & 0x00FF00FF) << 8)   |  ((x &  0xFF00FF00) >> 8);
    if (shamt & 16) x |= ((x & 0x0000FFFF) << 16) |  ((x &  0xFFFF0000) >> 16);
    return x;
}
uint64_t gorc64(uint64_t RA, uint64_t RB)
{
    uint64_t x = RA;
    int shamt = RB & 63;
    if (shamt & 1) x |= ((x & 0x5555555555555555LL)   <<   1) |
                         ((x & 0xAAAAAAAAAAAAAAAALL)  >>  1);
    if (shamt & 2) x |= ((x & 0x3333333333333333LL)   <<   2) |
                         ((x & 0xCCCCCCCCCCCCCCCCLL)  >>  2);
    if (shamt & 4) x |= ((x & 0x0F0F0F0F0F0F0F0FLL)   <<   4) |
                         ((x & 0xF0F0F0F0F0F0F0F0LL)  >>  4);
    if (shamt & 8) x |= ((x & 0x00FF00FF00FF00FFLL)   <<   8) |
                         ((x & 0xFF00FF00FF00FF00LL)  >>  8);
    if (shamt & 16) x |= ((x & 0x0000FFFF0000FFFFLL)  << 16) |
                         ((x & 0xFFFF0000FFFF0000LL)  >> 16);
    if (shamt & 32) x |= ((x & 0x00000000FFFFFFFFLL)  << 32) |
                         ((x & 0xFFFFFFFF00000000LL)  >> 32);
    return x;
}

xperm

based on RV bitmanip.

RA contains a vector of indices to select parts of RB to be copied to RT. The immediate-variant allows up to an 8 bit pattern (repeated) to be targetted at different parts of RT.

xperm shares some similarity with one of the uses of bmator in that xperm indices are binary addressing where bitmator may be considered to be unary addressing.

uint_xlen_t xpermi(uint8_t imm8, uint_xlen_t RB, int sz_log2)
{
    uint_xlen_t r = 0;
    uint_xlen_t sz = 1LL << sz_log2;
    uint_xlen_t mask = (1LL << sz) - 1;
    uint_xlen_t RA = imm8 | imm8<<8 | ... | imm8<<56;
    for (int i = 0; i < XLEN; i += sz) {
        uint_xlen_t pos = ((RA >> i) & mask) << sz_log2;
        if (pos < XLEN)
            r |= ((RB >> pos) & mask) << i;
    }
    return r;
}
uint_xlen_t xperm(uint_xlen_t RA, uint_xlen_t RB, int sz_log2)
{
    uint_xlen_t r = 0;
    uint_xlen_t sz = 1LL << sz_log2;
    uint_xlen_t mask = (1LL << sz) - 1;
    for (int i = 0; i < XLEN; i += sz) {
        uint_xlen_t pos = ((RA >> i) & mask) << sz_log2;
        if (pos < XLEN)
            r |= ((RB >> pos) & mask) << i;
    }
    return r;
}
uint_xlen_t xperm_n (uint_xlen_t RA, uint_xlen_t RB)
{  return xperm(RA, RB, 2); }
uint_xlen_t xperm_b (uint_xlen_t RA, uint_xlen_t RB)
{  return xperm(RA, RB, 3); }
uint_xlen_t xperm_h (uint_xlen_t RA, uint_xlen_t RB)
{  return xperm(RA, RB, 4); }
uint_xlen_t xperm_w (uint_xlen_t RA, uint_xlen_t RB)
{  return xperm(RA, RB, 5); }

bitmatrix

uint64_t bmatflip(uint64_t RA)
{
    uint64_t x = RA;
    x = shfl64(x, 31);
    x = shfl64(x, 31);
    x = shfl64(x, 31);
    return x;
}
uint64_t bmatxor(uint64_t RA, uint64_t RB)
{
    // transpose of RB
    uint64_t RBt = bmatflip(RB);
    uint8_t u[8]; // rows of RA
    uint8_t v[8]; // cols of RB
    for (int i = 0; i < 8; i++) {
        u[i] = RA >> (i*8);
        v[i] = RBt >> (i*8);
    }
    uint64_t x = 0;
    for (int i = 0; i < 64; i++) {
        if (pcnt(u[i / 8] & v[i % 8]) & 1)
            x |= 1LL << i;
    }
    return x;
}
uint64_t bmator(uint64_t RA, uint64_t RB)
{
    // transpose of RB
    uint64_t RBt = bmatflip(RB);
    uint8_t u[8]; // rows of RA
    uint8_t v[8]; // cols of RB
    for (int i = 0; i < 8; i++) {
        u[i] = RA >> (i*8);
        v[i] = RBt >> (i*8);
    }
    uint64_t x = 0;
    for (int i = 0; i < 64; i++) {
        if ((u[i / 8] & v[i % 8]) != 0)
            x |= 1LL << i;
    }
    return x;
}
uint64_t bmatand(uint64_t RA, uint64_t RB)
{
    // transpose of RB
    uint64_t RBt = bmatflip(RB);
    uint8_t u[8]; // rows of RA
    uint8_t v[8]; // cols of RB
    for (int i = 0; i < 8; i++) {
        u[i] = RA >> (i*8);
        v[i] = RBt >> (i*8);
    }
    uint64_t x = 0;
    for (int i = 0; i < 64; i++) {
        if ((u[i / 8] & v[i % 8]) == 0xff)
            x |= 1LL << i;
    }
    return x;
}

Introduction to Carry-less and GF arithmetic

There are three completely separate types of Galois-Field-based arithmetic that we implement which are not well explained even in introductory literature. A slightly oversimplified explanation is followed by more accurate descriptions:

  • GF(2) carry-less binary arithmetic. this is not actually a Galois Field, but is accidentally referred to as GF(2) - see below as to why.
  • GF(p) modulo arithmetic with a Prime number, these are "proper" Galois Fields
  • GF(2^N) carry-less binary arithmetic with two limits: modulo a power-of-2 (2N) and a second "reducing" polynomial (similar to a prime number), these are said to be GF(2N) arithmetic.

further detailed and more precise explanations are provided below

  • Polynomials with coefficients in GF(2) (aka. Carry-less arithmetic -- the cl* instructions). This isn't actually a Galois Field, but its coefficients are. This is basically binary integer addition, subtraction, and multiplication like usual, except that carries aren't propagated at all, effectively turning both addition and subtraction into the bitwise xor operation. Division and remainder are defined to match how addition and multiplication works.
  • Galois Fields with a prime size (aka. GF(p) or Prime Galois Fields -- the gfp* instructions). This is basically just the integers mod p.
  • Galois Fields with a power-of-a-prime size (aka. GF(p^n) or GF(q) where q == p^n for prime p and integer n > 0). We only implement these for p == 2, called Binary Galois Fields (GF(2^n) -- the gfb* instructions). For any prime p, GF(p^n) is implemented as polynomials with coefficients in GF(p) and degree < n, where the polynomials are the remainders of dividing by a specificly chosen polynomial in GF(p) called the Reducing Polynomial (we will denote that by red_poly). The Reducing Polynomial must be an irreducable polynomial (like primes, but for polynomials), as well as have degree n. All GF(p^n) for the same p and n are isomorphic to each other -- the choice of red_poly doesn't affect GF(p^n)'s mathematical shape, all that changes is the specific polynomials used to implement GF(p^n).

Many implementations and much of the literature do not make a clear distinction between these three categories, which makes it confusing to understand what their purpose and value is.

  • carry-less multiply is extremely common and is used for the ubiquitous CRC32 algorithm. [TODO add many others, helps justify to ISA WG]
  • GF(2N) forms the basis of Rijndael (the current AES standard) and has significant uses throughout cryptography
  • GF(p) is the basis again of a significant quantity of algorithms (TODO, list them, jacob knows what they are), even though the modulo is limited to be below 64-bit (size of a scalar int)

Instructions for Carry-less Operations

aka. Polynomials with coefficients in GF(2)

Carry-less addition/subtraction is simply XOR, so a cladd instruction is not provided since the xor[i] instruction can be used instead.

These are operations on polynomials with coefficients in GF(2), with the polynomial's coefficients packed into integers with the following algorithm:

Carry-less Multiply Instructions

based on RV bitmanip see https://en.wikipedia.org/wiki/CLMUL_instruction_set and https://www.felixcloutier.com/x86/pclmulqdq and https://en.m.wikipedia.org/wiki/Carry-less_product

They are worth adding as their own non-overwrite operations (in the same pipeline).

clmul Carry-less Multiply

clmulh Carry-less Multiply High

clmulr Carry-less Multiply (Reversed)

Useful for CRCs. Equivalent to bit-reversing the result of clmul on bit-reversed inputs.

clmadd Carry-less Multiply-Add

clmadd RT, RA, RB, RC

(RT) = clmul((RA), (RB)) ^ (RC)

cltmadd Twin Carry-less Multiply-Add (for FFTs)

Used in combination with SV FFT REMAP to perform a full Discrete Fourier Transform of Polynomials over GF(2) in-place. Possible by having 3-in 2-out, to avoid the need for a temp register. RS is written to as well as RT.

Note: Polynomials over GF(2) are a Ring rather than a Field, so, because the definition of the Inverse Discrete Fourier Transform involves calculating a multiplicative inverse, which may not exist in every Ring, therefore the Inverse Discrete Fourier Transform may not exist. (AFAICT the number of inputs to the IDFT must be odd for the IDFT to be defined for Polynomials over GF(2). TODO: check with someone who knows for sure if that's correct.)

cltmadd RT, RA, RB, RC

TODO: add link to explanation for where RS comes from.

a = (RA)
c = (RC)
# read all inputs before writing to any outputs in case
# an input overlaps with an output register.
(RT) = clmul(a, (RB)) ^ c
(RS) = a ^ c

cldivrem Carry-less Division and Remainder

cldivrem isn't an actual instruction, but is just used in the pseudo-code for other instructions.

cldiv Carry-less Division

cldiv RT, RA, RB

n = (RA)
d = (RB)
q, r = cldivrem(n, d, width=XLEN)
(RT) = q

clrem Carry-less Remainder

clrem RT, RA, RB

n = (RA)
d = (RB)
q, r = cldivrem(n, d, width=XLEN)
(RT) = r

Instructions for Binary Galois Fields GF(2^m)

see:

Binary Galois Field addition/subtraction is simply XOR, so a gfbadd instruction is not provided since the xor[i] instruction can be used instead.

GFBREDPOLY SPR -- Reducing Polynomial

In order to save registers and to make operations orthogonal with standard arithmetic, the reducing polynomial is stored in a dedicated SPR GFBREDPOLY. This also allows hardware to pre-compute useful parameters (such as the degree, or look-up tables) based on the reducing polynomial, and store them alongside the SPR in hidden registers, only recomputing them whenever the SPR is written to, rather than having to recompute those values for every instruction.

Because Galois Fields require the reducing polynomial to be an irreducible polynomial, that guarantees that any polynomial of degree > 1 must have the LSB set, since otherwise it would be divisible by the polynomial x, making it reducible, making whatever we're working on no longer a Field. Therefore, we can reuse the LSB to indicate degree == XLEN.

gfbredpoly -- Set the Reducing Polynomial SPR GFBREDPOLY

unless this is an immediate op, mtspr is completely sufficient.

gfbmul -- Binary Galois Field GF(2^m) Multiplication

gfbmul RT, RA, RB

gfbmadd -- Binary Galois Field GF(2^m) Multiply-Add

gfbmadd RT, RA, RB, RC

gfbtmadd -- Binary Galois Field GF(2^m) Twin Multiply-Add (for FFT)

Used in combination with SV FFT REMAP to perform a full GF(2^m) Discrete Fourier Transform in-place. Possible by having 3-in 2-out, to avoid the need for a temp register. RS is written to as well as RT.

gfbtmadd RT, RA, RB, RC

TODO: add link to explanation for where RS comes from.

a = (RA)
c = (RC)
# read all inputs before writing to any outputs in case
# an input overlaps with an output register.
(RT) = gfbmadd(a, (RB), c)
# use gfbmadd again since it reduces the result
(RS) = gfbmadd(a, 1, c) # "a * 1 + c"

gfbinv -- Binary Galois Field GF(2^m) Inverse

gfbinv RT, RA

Instructions for Prime Galois Fields GF(p)

GFPRIME SPR -- Prime Modulus For gfp* Instructions

gfpadd Prime Galois Field GF(p) Addition

gfpadd RT, RA, RB

the addition happens on infinite-precision integers

gfpsub Prime Galois Field GF(p) Subtraction

gfpsub RT, RA, RB

the subtraction happens on infinite-precision integers

gfpmul Prime Galois Field GF(p) Multiplication

gfpmul RT, RA, RB

the multiplication happens on infinite-precision integers

gfpinv Prime Galois Field GF(p) Invert

gfpinv RT, RA

Some potential hardware implementations are found in: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.90.5233&rep=rep1&type=pdf

gfpmadd Prime Galois Field GF(p) Multiply-Add

gfpmadd RT, RA, RB, RC

the multiplication and addition happens on infinite-precision integers

gfpmsub Prime Galois Field GF(p) Multiply-Subtract

gfpmsub RT, RA, RB, RC

the multiplication and subtraction happens on infinite-precision integers

gfpmsubr Prime Galois Field GF(p) Multiply-Subtract-Reversed

gfpmsubr RT, RA, RB, RC

the multiplication and subtraction happens on infinite-precision integers

gfpmaddsubr Prime Galois Field GF(p) Multiply-Add and Multiply-Sub-Reversed (for FFT)

Used in combination with SV FFT REMAP to perform a full Number-Theoretic-Transform in-place. Possible by having 3-in 2-out, to avoid the need for a temp register. RS is written to as well as RT.

gfpmaddsubr RT, RA, RB, RC

TODO: add link to explanation for where RS comes from.

factor1 = (RA)
factor2 = (RB)
term = (RC)
# read all inputs before writing to any outputs in case
# an input overlaps with an output register.
(RT) = gfpmadd(factor1, factor2, term)
(RS) = gfpmsubr(factor1, factor2, term)

Already in POWER ISA or subsumed

Lists operations either included as part of other bitmanip operations, or are already in Power ISA.

cmix

based on RV bitmanip, covered by ternlog bitops

uint_xlen_t cmix(uint_xlen_t RA, uint_xlen_t RB, uint_xlen_t RC) {
    return (RA & RB) | (RC & ~RB);
}

count leading/trailing zeros with mask

in v3.1 p105

count = 0
do i = 0 to 63 if((RB)i=1) then do
if((RS)i=1) then break end end count ← count + 1
RA ← EXTZ64(count)

bit deposit

pdepd VRT,VRA,VRB, identical to RV bitmamip bdep, found already in v3.1 p106

do while(m < 64)
   if VSR[VRB+32].dword[i].bit[63-m]=1 then do
      result = VSR[VRA+32].dword[i].bit[63-k]
      VSR[VRT+32].dword[i].bit[63-m] = result
      k = k + 1
   m = m + 1


uint_xlen_t bdep(uint_xlen_t RA, uint_xlen_t RB)
{
    uint_xlen_t r = 0;
    for (int i = 0, j = 0; i < XLEN; i++)
        if ((RB >> i) & 1) {
            if ((RA >> j) & 1)
                r |= uint_xlen_t(1) << i;
            j++;
        }
    return r;
}

bit extract

other way round: identical to RV bext: pextd, found in v3.1 p196

uint_xlen_t bext(uint_xlen_t RA, uint_xlen_t RB)
{
    uint_xlen_t r = 0;
    for (int i = 0, j = 0; i < XLEN; i++)
        if ((RB >> i) & 1) {
            if ((RA >> i) & 1)
                r |= uint_xlen_t(1) << j;
            j++;
        }
    return r;
}

centrifuge

found in v3.1 p106 so not to be added here

ptr0 = 0
ptr1 = 0
do i = 0 to 63
    if((RB)i=0) then do
       resultptr0 = (RS)i
    end 
    ptr0 = ptr0 + 1
    if((RB)63-i==1) then do
        result63-ptr1 = (RS)63-i
    end
    ptr1 = ptr1 + 1
RA = result

bit to byte permute

similar to matrix permute in RV bitmanip, which has XOR and OR variants, these perform a transpose (bmatflip). TODO this looks VSX is there a scalar variant in v3.0/1 already

do j = 0 to 7
  do k = 0 to 7
     b = VSR[VRB+32].dword[i].byte[k].bit[j]
     VSR[VRT+32].dword[i].byte[j].bit[k] = b

Appendix

see appendix